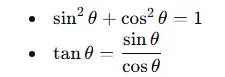三角比という言葉を聞くと、それだけで少し肩に力が入ってしまう高校1年生はとても多いです。
特に数学があまり得意ではない人にとって、いきなり sin や cos や tan が並ぶノートは「自分には無理かも…」と感じやすい単元です。
でも安心してください。
三角比は、本当はただの
「直角三角形の辺の比の名前」
にすぎません。
このガイドでは、難しい公式を丸暗記するのではなく、図を使ってイメージから積み上げる方法で、sin・cos・tan の意味とテストで使える勉強法までを一気に整理していきます。
三角比が「急に難しく感じる」本当の理由
三角比の単元に入ったとき、多くの高校1年生が同じパターンでつまずきます。
その原因は、あなたの理解力ではなく、「説明の順番」にあります。
ありがちな三角比のつまずきパターン
- sin・cos・tan の定義をちゃんと聞く前に、
いきなり
「sin30°=1/2、sin45°=√2/2、sin60°=√3/2…」
と値だけ暗記しようとしてしまう。 - 直角三角形の図は見たけれど、
どの辺が「対辺」でどの辺が「底辺」なのかが曖昧なまま先に進んでしまう。 - 問題を見たときに、
「これは sin?cos?tan?どれを使うの?」という“公式当てクイズ”状態になってしまう。
こうなると、三角比は一気に
「公式が多すぎる謎の暗記ゲーム」
に見えてしまいます。
しかし、本来の三角比は
- 直角三角形
- 3本の辺の長さ
- その比の名前(sin・cos・tan)
がきれいに結びついた、とてもシンプルな道具です。
【結論】: 三角比が難しく感じるときは、公式を覚える前に「直角三角形の図」と「辺の名前」に必ず一度立ち返ってください。
なぜなら、数学が苦手な生徒ほど、式だけをノートに詰め込んでしまい、図と意味が頭の中でつながっていないことが多いからです。直角三角形のイメージがはっきりすれば、sin・cos・tan は「どの比の名前か」を落ち着いて選べるようになります。この知見が、三角比アレルギーを和らげるきっかけになればうれしいです。
三角比とは?「直角三角形の辺の比の名前」だけ覚えよう
三角比の本当の正体は、とてもシンプルです。
三角比 = 直角三角形の 3 つの辺の比の名前
まずはこの一文だけを、ノートの一番上に大きく書いておいてください。
直角三角形と三つの辺の名前
角度が θ(シータ)の直角三角形を 1 つ用意します。
すると、3 本の辺にはそれぞれ次のような役割があります。
- 斜辺:直角をはさんでいない、一番長い辺
- 対辺:角 θ の「向かい側」にある辺
- 底辺:角 θ の「足もと」にある辺(角 θ に隣り合う直角ではない辺)
この 3 本の辺を使って、三角比は次のように定義されます。
- sin θ(サイン) = 対辺 ÷ 斜辺
- cos θ(コサイン) = 底辺 ÷ 斜辺
- tan θ(タンジェント) = 対辺 ÷ 底辺
つまり、三角比は
「どの 2 本の辺の“比”を見ているかを教えてくれるラベル」
だと考えることができます。
三角比と sin・cos・tan の関係
ここで、エンティティどうしの関係を整理すると、頭がすっきりします。
- 三角比は、sin θ・cos θ・tan θ の 3 つの比の総称です。
- sin θは、直角三角形の対辺と斜辺の比を表します。
- cos θは、直角三角形の底辺と斜辺の比を表します。
- tan θは、直角三角形の対辺と底辺の比を表します。
三角比という大きな箱の中に、sin・cos・tan の 3 兄弟が入っているイメージを持つと理解しやすくなります。
🎨 デザイナー向け指示書:インフォグラフィック
件名: 直角三角形と三角比(sin・cos・tan)の関係図
目的: 三角比が直角三角形の 3 本の辺の比から定義されることと、sin・cos・tan がそれぞれどの辺の比なのかを一目で理解できるようにする。
構成要素:
- タイトル: 「三角比は『直角三角形の辺の比の名前』」
- メイン図:
- 1 つの直角三角形を中央に配置する。
- 角 θ を左下に配置し、そこから反時計回りに 3 つの辺を
- 斜辺(上側の斜めの辺)
- 対辺(右側の縦の辺)
- 底辺(左下から右下の横の辺)
とラベル付けする。
- 斜辺・対辺・底辺をそれぞれ異なる色で塗る。
- sin・cos・tan のボックス:
- 図の下部に 3 つのボックスを横並びに配置する。
- 左から順に
- sin θ = 対辺 ÷ 斜辺(対辺と斜辺の色をミニ矩形で並べる)
- cos θ = 底辺 ÷ 斜辺(底辺と斜辺の色)
- tan θ = 対辺 ÷ 底辺(対辺と底辺の色)
- 各ボックスに小さなキャラクターアイコン(sin・cos・tan の 3 兄弟)を添えて親しみやすさを出す。
- 補足:
- 図の余白に「三角比=この 3 つの比のセット」と短い吹き出しを追加する。
デザインの方向性:
シンプルでフラットなイラスト。線はやや太めで、色は 3 色(例:青=斜辺、ピンク=対辺、緑=底辺)+モノトーン。スマホ画面でも視認性が高いコントラストを意識する。
参考 alt テキスト案:
「直角三角形の斜辺・対辺・底辺を色分けし、sin θ=対辺/斜辺、cos θ=底辺/斜辺、tan θ=対辺/底辺という三角比の定義を図解したイラスト」
テストで点につながる三角比の「3ステップ勉強法」
ここからは、三角比をテストで点数につなげるための具体的な勉強の順番を整理します。
結論から言うと、三角比は次の 3 ステップで学ぶと、もっとも効率よく身につきます。
- 有名角の三角比を「2つの三角形」から作る
- 三角比の相互関係を「家系図」で整理する
- 10分 × 3 セットのミニ演習で定着させる
Step1:2つの三角形から有名角の三角比を作る
テストで頻出の「有名角」は次の角度です。
- 0°
- 30°
- 45°
- 60°
- 90°
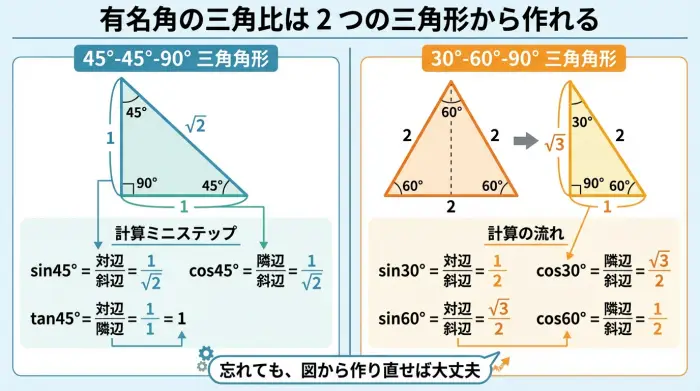
このうち、30°・45°・60° の三角比は、たった 2 つの三角形から作ることができます。
- 直角二等辺三角形(45°用)
- 正三角形を半分にした三角形(30°・60°用)
これらの三角形で辺の長さの比を考えることで、sin・cos・tan の値を公式として暗記するのではなく、自分の手で再現できるようにすることが大切です。
【結論】: 有名角の三角比は、「表を丸暗記」ではなく「2つの三角形から再現できるように練習する」ほうが、結果的にラクになります。
なぜなら、テスト本番で一部の値を忘れてしまっても、図から導く方法を知っている生徒は、慌てずに計算で復元できるからです。丸暗記だけに頼ると、「思い出せない=詰み」になりやすく、緊張したときほどリスクが高くなります。
Step2:三角比の相互関係を「家系図」にする
三角比どうしには、次のような有名な関係があります。
この 2 つの式は、テストで非常によく出題されます。
三角比と三角比の関係を、家系図のようなイメージでつないで整理しておくと、公式を忘れにくくなります。
- sin と cos は「二乗して足すと 1 になる姉妹」のような関係。
- tan は「sin と cos の比でできている兄弟」のような関係。
三角比の相互関係は、有名角の値を組み合わせた計算問題の裏で必ず動いている仕組みなので、図でまとめておくと安心です。
Step3:10分 × 3 セットのミニ演習で定着させる
最後に、テスト前の勉強メニューを、1 日 30 分のセットに分解して提案します。
- 10分:定義の確認
- sin・cos・tan の定義をノートに書き写しながら、図を毎回一緒に描く。
- 10分:有名角の再現
- 直角二等辺三角形と正三角形の半分を使って、有名角の三角比の表を自分で作る。
- 10分:典型問題の演習
- 教科書や問題集から、三角比の基本問題を 5〜10 題ほど解き、解説をしっかり読む。
この 3 ステップをテスト前 3〜4 日連続で繰り返すだけでも、基礎点の取りこぼしはかなり減ります。
| 勉強法 | 覚えやすさ | 忘れにくさ | テスト本番での安心感 | 特徴 |
|---|---|---|---|---|
| 有名角の値だけを丸暗記する勉強 | 最初は早く覚えられる | 一度崩れると一気に不安になる | 緊張すると思い出せないことが多い | ノートに公式の羅列が増えやすく、図や意味が残りにくい |
| 三角形から有名角を導く勉強 | 最初は少し時間がかかる | 図を見れば思い出せるため長持ちする | 忘れてもその場で導き直せるので安心感が高い | 図と三角比の関係が頭に残り、応用問題にも強くなる |
三角比のよくある疑問Q&A(テスト前にチェック)
最後に、三角比でよく出てくる疑問を Q&A 形式でまとめておきます。
テスト前に、ここだけ読み返しても OK です。
Q1. sin と cos の違いを一言でいうと?
A.
sin は「対辺 ÷ 斜辺」の比で、cos は「底辺 ÷ 斜辺」の比です。
どちらも「斜辺で割る」という点は同じですが、分子の辺が違うため、角 θ から見てどの辺を “縦” とみなすかというイメージが変わります。
Q2. tan はいつ使えばいいですか?
A.
tan は「対辺 ÷ 底辺」の比なので、斜辺が登場しない問題で力を発揮します。
また、tan は という関係を持っているので、sin と cos から tan を作ることもできます。
Q3. 有名角を全部覚えられないとダメですか?
A.
理想は覚えておくことですが、2つの三角形から導けるようになっていれば大丈夫です。
30°・45°・60° の三角比を自分で再現できるようにしておけば、テスト本番で一部を忘れても落ち着いて計算で復元できます。
Q4. 三角比が分からないと、三角関数は絶対に無理ですか?
A.
三角関数は、三角比を「角度の変化に応じて連続的に扱う」ところから始まります。
三角比が
- 直角三角形の辺の比の名前であること
- sin・cos・tan の意味
- 有名角の値
この 3 点が押さえられていれば、三角関数のスタートラインにはしっかり立てています。
Q5. 公式が多すぎて不安です…
A.
三角比で「絶対に押さえておきたい公式」は、実は次の 3 つです。
- sin θ = 対辺 ÷ 斜辺
- cos θ = 底辺 ÷ 斜辺
- tan θ = 対辺 ÷ 底辺(= sin θ ÷ cos θ)
あとは、有名角の値と が加われば、定期テストの基本問題には十分対応できます。
まとめと次の一歩
最後に、このガイドで整理したポイントをもう一度確認します。
- 三角比とは、直角三角形の 3 本の辺の比の名前です。
- sin θ は対辺 ÷ 斜辺、cos θ は底辺 ÷ 斜辺、tan θ は対辺 ÷ 底辺です。
- 有名角(30°・45°・60°)の三角比は、直角二等辺三角形と正三角形の半分から導くことができます。
- 三角比どうしには、 や などの相互関係があります。
- テスト前は、「定義の確認 → 有名角の再現 → 典型問題の演習」の 10 分 × 3 セット勉強が効果的です。
あなたがこの記事を読みながら作ったノートは、これからの三角比の勉強におけるホームベースになります。
迷ったときは、またこのノートと「直角三角形の図」に戻ってきてください。
今日の行動目標
- ノートに「三角比まとめページ」を 1 ページ作る。
- 直角二等辺三角形と正三角形の半分の図を描き、有名角の三角比を自分で導いてみる。
- 教科書や問題集から三角比の基本問題を 5 題だけ解いてみる。
この 3 つができれば、あなたはもう「三角比がよくわからない人」から一歩抜け出しています。